Почти линейная сложность решения NP-полной задачи планирования производства
В статье приведено описание подхода к решению задачи планирования производства в существующей и работающей системе APS ТАП. Показано теоретическое обоснование высокой скорости работы системы. Приведен подход, сводящий сложность задачи из области конструирования алгоритма в область подбора функций специального вида. Данный подход потенциально может оказать влияние на пути решения сложных задач, в том числе эквивалентности классов P и NP.
Традиционно путь от идеи до ее воплощения выглядит так, словно вначале в статье описывается идея, затем по ней возникает воплощение. Однако на практике обычно всё наоборот и статья является лишь подведением итогов работы. Не будем отступать от реальности. В этой статье изложены результаты реализации системы планирования. Задача планирования производства хорошо известна, состоит из двух связанных подзадач - составления списка всех работ (разузлования) и составления расписания, то есть планирования этих работ на исполнители, и достаточно хорошо описана, например, в классическом труде Пинедо.
Из-за ее высокой трудоемкости обычно процесс решения доводят до некоторого уровня группировки заданий, как это делается при объемно-календарном планировании в SAP, однако конечной целью процесса планирования является получение списка привязанных к исполнителям элементарных работ - плана работ, из которых можно формировать сменно-суточные задания.
В качестве входных данных следует рассматривать список заказов, исполнителей (станков и рабочих мест) и техпроцессы. Отдельный техпроцесс описывает линейный процесс получения детали, однако все техпроцессы образуют древовидную структуру, описывающую процесс изготовления заказа. Конечно, нужно учитывать и незавершенное производство и управление временем в виде календарей и многие другие ньюансы, без учета которых невозможно построить рабочий план.
Обычно задача планирования ставится как задача оптимизации - как минимум по затраченному времени для производства заказа. Однако на практике могут оказатся важными иные критерии - уровень загрузки производства, время пролёживания полуфабрикатов на складах и многие другие. Поэтому правильнее будет говорить, что задана некоторая функция, вычислимая над планом работ, чьё значение нужно оптимизировать (для определенности - минимизировать). Именно в такой постановке и была решена задача планирования в системе APS ТАП .
Известно, что в общем случае задача оптимального планирования относится к классу NP-полных задач и не существует быстрого способа получить ее решение. Поэтому существующие методы решения опираются на различные эвристики. Не является исключением и построенная система APS - она также опирается на множество эвристик. Однако ключевым отличием ее является собственно алгоритм работы.
В общем виде ее работу можно описать как двух-этапный процесс. На первом этапе формируется упорядоченный список элементарных работ. Так как такие работы связаны между собой отношением последовательности (одна работа должна строго предшествовать другой работе, как это следует из техпроцесса, но работы из разных техпроцессов не имеют такой явной связи), то и такая линейная структура частично упорядочена. На втором этапе из нее формируется план работ путем привязки к времени и исполнителю. Работа по построению списка на первом этапе производится рекурсивным применением некоторых функций, каждое применение добавляет в конец списка набор работ и общий объем вычислений линеен относительно количества элементов очереди.
Второй этап можно рассматривать как отображение очереди работ в другую очередь привязанных к исполнителю работ, не меняющее количество элементов очереди, но, возможно, меняющее порядок ее элементов. Очевидно, это сюрьективное отображение. Именно здесь производится привязка работ к исполнителям и назначается время начала и завершения. Особенностью такого подхода является следующее. Порядок работ, в котором они формируются на первом этапе, определяет сложность работы второго этапа и оптимальность полученного результата. Оказывается, это порядок может быть устроен так, что второй этап допускает обработку всего в один проход, то есть каждый элемент просматривается только один раз.
Более того, и оптимальность в смысле выбранного функционала также реализуется определенной упорядоченностью этого списка.
В самом деле, предположим, что мы имеем уже оптимальный план работ. Второй этап процесса планирования получил его из некоторой очереди заданий реализуемым способом. В силу свойств второго этапа существует как минимум одна очередь заданий, из которой получается оптимальный план. И, стало быть вопрос поиска оптимального план производства оказывается сведен к поиску функций, обеспечивающих необходимое упорядочивание очереди заданий после первого этапа.
Конечно, вопрос существования таких функций остается открытым. Однако само существование и работоспособность система APS ТАП доказывает, что такие функции можно подобрать, причем они дают лучшие результаты относительно известных иных способов решения этой задачи.
Из-за сложной структуры техпроцессов построить оценку сложности задачи в зависимости от входных данных очень затруднительно, если вообще возможно. Происходит это из-за различий в структуре дерева техпроцессов. В простейшем случае одного линейного техпроцесса сложность задачи можно оценить от размера входных данных - количества деталей в заказе и длины техпроцесса. Заметим, что в этом случае длина плата работ пропорциональна входным данным. Поэтому предлагается оценивать сложность решения по размеру формируемого плана работ, так как размер этого плана при заданных входных данных фиксирован, а для получения каждого его элемента требуется произвести вычисления.
Конечно, это не NP-сложность оптимального плана работ, но дает представление об эффективности полученного решения. Для реализованного алгоритма в системе APS такого рода оценка дает O(N *log(N)), то есть практически линейную сложность от размера вычисленного плана работ. В самом деле, первый этап реализован так, что затрачивает константное количество вычислений на единицу очереди задач, а на втором этапе производится лишь один просмотр очереди и для каждого элемента производится бинарный поиск с целью привязки по времени. Бинарный поиск производится среди не более N отрезков( на самом деле, конечно, гораздо меньше) - как результат, сложность этого O(log(N)).
Кроме того, оказывается возможным ввести параметры типа оптимальной партии запуска, размера выходного буфера станка и некоторые другие. Это позволяет говорить о том, что решение является параметризованным.
Из-за высокой скорости работы и наличия параметризации такой подход позволяет гибко управлять получаемым решением и даже организовывать процедуры поиска оптимальных решений, например, применением известных методов поиска оптимум - генетический алгоритм, градиентные методы и т.д.
Так как в статье обсуждалась уже созданная и работающая система APS, то будет интересно привести ее результаты работы.
Итак, результаты работы системы APS . Все вычисления проводились на одном процессоре (частота 3.5 ГГц) с достаточным количеством оперативной памяти (16 Гбайт). В таблице указаны общие параметры заданий - глубина дерева технологий, средний размер техпроцесса (среднее число шагов техпроцесса), размер полученного плана работ. Приведены данные по характерным практическим вариантам использования (за каждым стоит реальное производство).
| Размер заказа | Глубина дерева техпроцессов | Средняя длинна техпроцесса | Размер плана работ, тыс. операций | Время вычисления |
|---|---|---|---|---|
| 20 | 6 | 3 | 585 | 11 секунд |
| 1440 | 5 | 19 | 3500 | 75 секунд |
| 5000 | 13 | 18 | 48000 | 118 секунд |
Как видно, время работы не превосходит 2 минут. Многочисленное тестирование, в том числе и на предельно большие значения выявило, что время работы колеблется от 0.1 до 200 секунд, в крайних случаях доходя до 20 минут. Причем в этом последнем случае из 20 минут 12 было потрачено на запись результата (был протестирован вариант с генерацией более миллиарда элементов плана).
Поскольку данная реализация показывает столь высокую скорость работы и имеет параметризацию, то в системе APS была реализована методика подбора параметров с целью оптимизации задаваемой пользователем целевой функции, причем последняя описывается в виде логического предиката самом пользователем.
Графики ниже иллюстрируют применение методов генетического алгоритма при оптимизации плана.
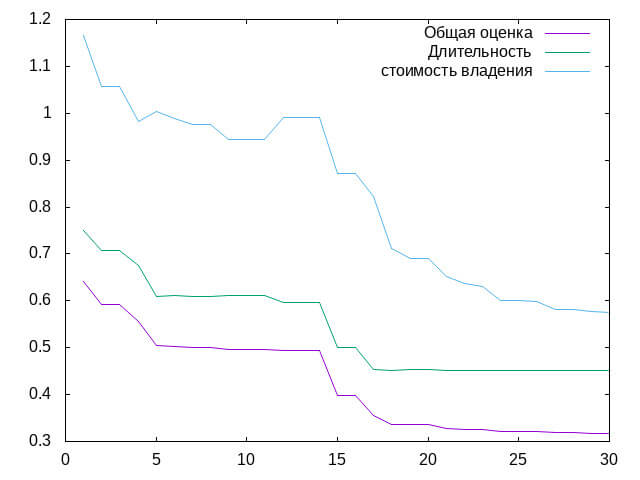
На них приведено, как изменяется общая оценка плана (линейный функционал), длительность самого плана и совокупная стоимость владения полуфабрикатами в процессе работы алгоритма (по оси Х приведены номера поколений). В примере было 103 параметра плана, 23 особи в популяции, 3 самых лучших оставались, 3 самых худших заменялись случайными, остальные подвергались случайной мутации.
Также параметризация позволила провести численные исследования того, как устроено пространство решений задачи. Для этого была взята задача с тремя параметрами с довольно типичным техпроцессом. Для каждого параметра была введена сетка значений, для каждой тройки значений был посчитан функционал от результата (он включал суммарное время выполнения плана, время пролеживания деталей на складах, суммарное время переналадок станков). Результат формировал кубик из точек, чей цвет и интенсивность отображают значение функционала.
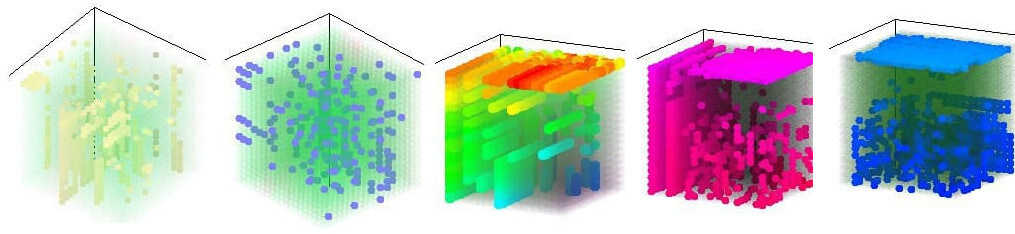
На рисунке приведены различные варианты отображения - в первом и втором слева обозначены точки локального минимума, что дает понимание, как устроено пространство решений задачи. Глобальный минимум находится на верхней грани почти в центре, как это видно на центральном рисунке. Два правых рисунке отображают срезы значений функционала.
Заключение
В разработанной системе планирования реализован новый подход в решении задач оптимального планирования со сложностью O(N*log(N)), причем задача построения оптимального плана сведена к проблеме нахождения вычислительных функций специального вида, что открывает новые возможности в решении NP-полных задач.
Автор: Олег Морозов, эксперт-математик.